i.e, the longest amount of time an algorithm can possibly take to complete. The notation O(n) is the formal way to express the upper bound (growth rate) of an algorithm's running time. The letter O is used because the rate of growth of a function is also called its order.
Let,
It implies,
Note:
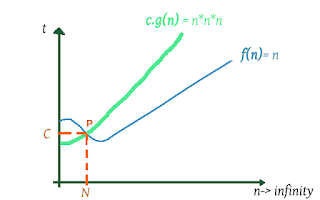 |
| Fig. 1.1. Time Complexity |
Therefore,
is a point on the x-axis where arbitrary vertical line PN is drawn.
- Right hand-side of arbitrary vertical line PN is
i.e.,
.
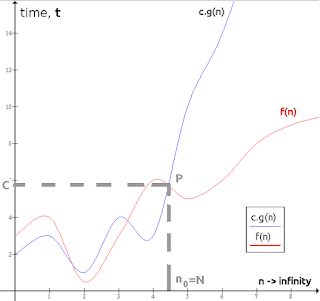 |
| Fig. 1.2. Example of Big O notation: f(n) ∈ O(g(n)) as there exists c > 0 (e.g., C = 4.9) and n0 (e.g., n0 =N= 4.3) such that f(n) ≤ cg(n) whenever n ≥ n0. |
Let's understand the concept more by solving some questions,
Q. 1.1. if given &space;=&space;3n&space;+&space;2) and
and =n) find
find  and
and  ?
?
Sol. we know the condition,
Thus, at 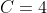 and
and 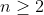 ,
, 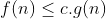 i.e.,
i.e., 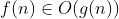 .
.
Note: We found that, for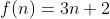 and
and 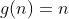 ,
, 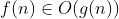 .
.
Note: We found that, for
Q.1.2 Prove that 1,000,000 n ) i.e., million
i.e., million )) .
.
Sol. To Prove:
Choose, C=1,000,000
Therefore, it doesn't matter where we place the arbitrary vertical line PN, as for any N this relationship will work.
Note:
\rightarrow) though it's mathematically good but not important while calculating Big-Oh.
though it's mathematically good but not important while calculating Big-Oh.
)) is exactly the same as
is exactly the same as )) . The logarithms differ only by a constant factor, and the big O notation ignores that. Similarly, logs with different constant bases are equivalent.
. The logarithms differ only by a constant factor, and the big O notation ignores that. Similarly, logs with different constant bases are equivalent.
Note:
- Big-Oh notation doesn't care about (most) constant factors. i.e., '
' - depends on the processor speed of the computer, not on the algorithm.
- So, '
' is not important. Big-Oh doesn't care about
, and it only tells about the efficiency of an Algorithm.
- If I say an Algorithm runs in
,
It doesn't mean the Algorithm is slow. Big-Oh is an upper bound only (as) .It is not a lower bound. i.e., It can say something is FAST but it can't say something is SLOW.
Q.1.3. Prove that ) .
.
Sol. Randomly set C=3, and N=1,Note: If we have SUM of functions, the one that grows faster dominates as we go further and further RHS of the arbitrary vertical line PN.
![Time Complexity of function [n^{3}] and [n^{2}] . Time Complexity of function [n^{3}] and [n^{2}] .](https://1.bp.blogspot.com/-tZOJuHfi40w/WRfZrs535QI/AAAAAAAAAi4/gRC2DnUG0mIcpkNFu896lKk5CdWFx1TLgCEw/s320/bigohexample.png) |
| Fig. 1.3. Time Complexity of function |
2. TABLE OF IMPORTANT BIG-OH SETS
 |
| Fig. 2.1. Table of important Big-Oh sets |
Smallest to largest.
- An algorithm with O(n log n) or faster time (above O(nlog n)) is considered to be "efficient".
- Algorithm with
or slower time (below
) are considered "useless".
- It also depends on how BIG the problem is. For instance,
for solving Rubik Cube is OK. As it's a very complicated problem. But,
for processing Database transaction in Google is NOT GOOD.
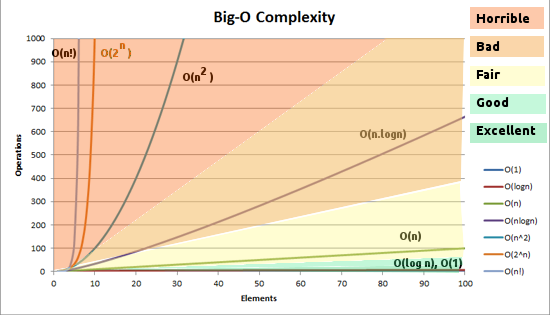 |
| Fig. 2.2. Simple graph to understand the Big-Oh complexity: The rate of growth of different function |
 |
| Fig. 2.3. Recap: Table of important Big-Oh sets. |
and
are significantly different.
grows faster, irrespective of how big the constant
is.
- Super-polynomial is functions that grow faster than any power of n.
- Sub-exponential are functions that grows slower than an exponential function,
.
- An algorithm can also take time that is both super-polynomial as well as sub-exponential. Ex: the fastest algorithms known for integer factorization.
3. WARNINGS
I. Fallacious Proof : If you are asked to prove
II. Big-Oh notation DOES NOT SAY what the functions are, it only expresses the relationship between two functions. You have to specify what those functions are.
Example: - Number of emails you send to your father w.r.t time is ) ,it implies: you are an increasingly good child.
,it implies: you are an increasingly good child.
Fact: BINARY SEARCH on an Array:
# Worst-case running time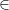 O(log n)
O(log n)
# Best-case running time) , when you get lucky & the 1st element was the one you were searching for.
, when you get lucky & the 1st element was the one you were searching for.
# Memory use) , stores all the value you are searching for.
, stores all the value you are searching for.
# Worst-case running time
# Best-case running time
# Memory use
Q.3.1. prove that ) ?
?
Sol.
Note: DON'T SAY that it's true because constant factors don't matter. Because by dividing we can prove that it's a fallacious statement! It's wrong!
Note: DON'T SAY that it's true because constant factors don't matter. Because by dividing we can prove that it's a fallacious statement! It's wrong!
Q.3.2. Prove that ) ?
?
Sol. Note: DON'T SAY that it's true because constant factors don't matter. Because by dividing we can prove that it's a fallacious statement! It's wrong!III. The Philosophical Idea (Its just FYI - not to be written in the exam): Big-Oh notation doesn't always tell the whole story.
Suppose, we have two different algorithms. Algorithm 1 runs in exactly
from the equation, its obvious that
Therefore, we can say that
Q.3.3. If analyzing an algorithm, one finds that time it takes to complete a problem of size '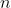 ' is given by
' is given by 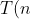=4n^{2}-2^{n}+2) . Find Big-Oh of this algorithm.
. Find Big-Oh of this algorithm.
Sol.- Ignoring constants (as it depends on the hardware on which it runs and not on the algorithm).
- Ignoring slower growing terms.
Thus,
Q.3.4 Prove &space;=&space;O(\sqrt{n})) .
.
Sol. We want c>0 and Any c>0 would work, the only problem is to find
So,
Thus we can take
Q.3.5. Is =O(log(n))) ?
?
Sol. We know, 4. Determining running time of a piece of code
To obtain the Big-Oh from a piece of code firstly we must realize that we will be creating a math formula to count how many steps of computations can get executed given an input of some size. i.e., It's an expression of how the execution time of a program scales with the input data. That is, as the input gets bigger, how much longer will the program take? Just a little bit? or a lot longer?
The running time depends on the kind of statements used in the code.
I. Statement sequence
Total time = sum of all the times of all the statements.
Total time = time(statement 1)+ time(statement 2)+...+time(statement n)
If all these statements are simple (i.e., involving basic operations) then the time for each statement is constant and the total time is also constant i.e., O(1).
II. Conditional Statements (if-else-if)
Here either 'block 1' will execute else 'block 2'. So, the worst-case time will be the slower block. If block 1 takes O(1) and block 2 takes O(N), the if-else-if would be O(N).
III. Loops
Here the loop will run N times. Therefore, statement sequence will also run N times. If these statements are simple then total time for these statements will be O(1). So, the total time for the loop is N*O(1) = O(N).
IV. Nested Loops
Here the outer-loop will run N times. And every time the outer loop runs the inner loop runs M times. So, the statement sequence will run N*M times. If these statements are simple then total time for these statements will be O(1). So, the total time for the loop is N*M*O(1) = O(N*M).
Special case: If M=N, then inner loop also runs N times every time the outer loop runs. So, total time would be=&space;N^{2}*O(1)=O(N^{2})) .
.
V. Function
Here if the function definition has simple statement sequence then it will take O(1) time. And since the function is in the loop which runs N times, the function will also run N time. So, total time = N*O(1) = O(N).
Now let's solve some questions:
Sol. Let's create a formula to find the computational complexity of the function sum which returns the sum of elements of the array. Let,
\rightarrow) be the function to count the number of computational steps.
be the function to count the number of computational steps.
i.e., the function that calculates the total number of steps.
 Input of the function i.e., the size of the structure to process.
Input of the function i.e., the size of the structure to process.
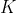 constant (O(1) terms), and the redundant part:
constant (O(1) terms), and the redundant part:
=1&space;+&space;N^{1}) Since, the last term is the one which grows bigger when
Since, the last term is the one which grows bigger when 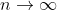 , our sum function has the time complexity of O(N).
, our sum function has the time complexity of O(N).
Sol. This is a search algorithm that breaks an array of numbers into half, to search a particular element i.e., with every iteration it divides the array into half. So, running time complexity is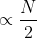 .
.
It is a type of divide and conquer algorithm. So it is)) .
.
Note: O(log n) basically means: time goes up linearly while n
if it takes
it will take
It is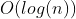 when we do divide and conquer type of
algorithms e.g binary search. Another example is quick sort where
when we do divide and conquer type of
algorithms e.g binary search. Another example is quick sort where
Sol. This is a small logic of Quick Sort algorithm. Now in Quick Sort, each time we divide the array into two parts and every time it takes O(N) time to find a pivot element. Hence it's n*log(n) i.e., O(n log n).
Note: In general, doing something with every element in 1D (i.e., one- dimension) is linear, doing something with every element in 2D is quadratic, and dividing the working area in half is logarithmic.
\rightarrow) is the set of functions that grow slower than or at the same rate as expression.
is the set of functions that grow slower than or at the same rate as expression.
I. Statement sequence
statement 1;
statement 2;
.
.
statement n; Total time = sum of all the times of all the statements.
Total time = time(statement 1)+ time(statement 2)+...+time(statement n)
If all these statements are simple (i.e., involving basic operations) then the time for each statement is constant and the total time is also constant i.e., O(1).
II. Conditional Statements (if-else-if)
if(condition){
//block 1
}
else{
//block 2
}III. Loops
for(i=1; i<N; i++){
//statement sequence;
} //end of loopIV. Nested Loops
for(i=1; i<N; i++){
for(j=1; j<M; j++){
//statement sequence;
} //end of loop
} //end of loopSpecial case: If M=N, then inner loop also runs N times every time the outer loop runs. So, total time would be
V. Function
for(robin=1; robin<N; robin++){
batmanCalling(robin); //function 1
}Now let's solve some questions:
Q.4.1. Find the computational complexity of the following code, where the function returns the sum of all the elements of the array:
int sum(int* data, int N) { int result = 0; // 1 for (int i = 0; i < N; i++) { // 2 result += data[i]; // 3 } return result; // 4} i.e., the function that calculates the total number of steps.
In laconic terms, Number of steps = ) .
.
Now, let's find the actual definition of the function) . This is done from the given source code.
. This is done from the given source code.
Assume that every sentence that doesn't depend on the size of the input data takes a constant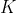 ' number computational steps.
' number computational steps.
Now, let's find the actual definition of the function
Assume that every sentence that doesn't depend on the size of the input data takes a constant
Lets' add the individual number of steps of the function. Variable declaration & return statement doesn't depend on the size of the data array.
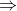 lines 1 and 4 takes '
lines 1 and 4 takes '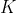 ' amount of steps each.Therefore,
' amount of steps each.Therefore,
&space;=&space;K+&space;....&space;+&space;K) The body of for loop executes
The body of for loop executes 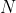 times, and the statement in the for loop body takes
times, and the statement in the for loop body takes 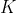 steps every time it's executed. So, it takes
steps every time it's executed. So, it takes 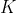 *
*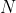 steps.
steps.
=K+(N*K)+K)
You have to count how many times the body of the for gets executed by looking at the code. We are ignoring the variable initialization, condition and increment parts of the for statement for simplicity.
To get the actual Big-Oh these are the general steps:
=2*K*N^{0}&space;+&space;K*N^{1})
Taking away all the To get the actual Big-Oh these are the general steps:
- Take away all the constants
. It is a.k.a C or O(1) terms.
- From
get the polynomial in its standard form.
- Divide the terms of the polynomial and sort them by the rate of growth.
- Keep the one that grows bigger when 'n' approaches infinity.
Q. 4.2. What is the time complexity of following code:
while(low <= high)
{
mid = (low + high) / 2;
if (target < list[mid])
high = mid - 1;
else if (target > list[mid])
low = mid + 1;
else break;
} Sol. This is a search algorithm that breaks an array of numbers into half, to search a particular element i.e., with every iteration it divides the array into half. So, running time complexity is
It is a type of divide and conquer algorithm. So it is
Note: O(log n) basically means: time goes up linearly while n
if it takes
1 second to compute 10 elements,it will take
2 seconds to compute 100 elements,3 seconds to compute 1000 elements, and so on...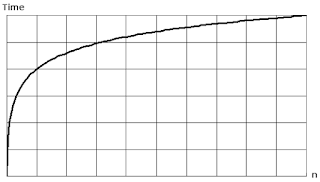 |
Fig 4.1 Example: Plotting log(n) on a plain piece of paper, will result in a graph where the rise of the curve decelerates as n increases |
It is
Q. 4.3. What is big-oh of following code:
void quicksort(int list[], int left, int right)
{
int pivot = partition(list, left, right);
quicksort(list, left, pivot - 1);
quicksort(list, pivot + 1, right);
}Sol. This is a small logic of Quick Sort algorithm. Now in Quick Sort, each time we divide the array into two parts and every time it takes O(N) time to find a pivot element. Hence it's n*log(n) i.e., O(n log n).
Note: In general, doing something with every element in 1D (i.e., one- dimension) is linear, doing something with every element in 2D is quadratic, and dividing the working area in half is logarithmic.

No comments
commentPost a Comment